先週から千葉入試が始まりました。
本命校として受ける方も、東京受験の練習校として受ける方もいらっしゃいます。
東京受験の練習校として受けた方はラッキーではないでしょうか。というのも、また今年、入試問題の難易度が上がったことを知ることで心の準備ができるからです。

上位校の難易度はそれほど変わりませんが、四谷大塚偏差値で52〜55あたりの中学校の問題は難しくなっている印象です。
今までだと、とにかく数字をかき集めてヒントを探す、がむしゃらに書き出して規則性の問題を解くやり方が通用していたのですが、今年はそのやり方では歯が立たないように感じます。

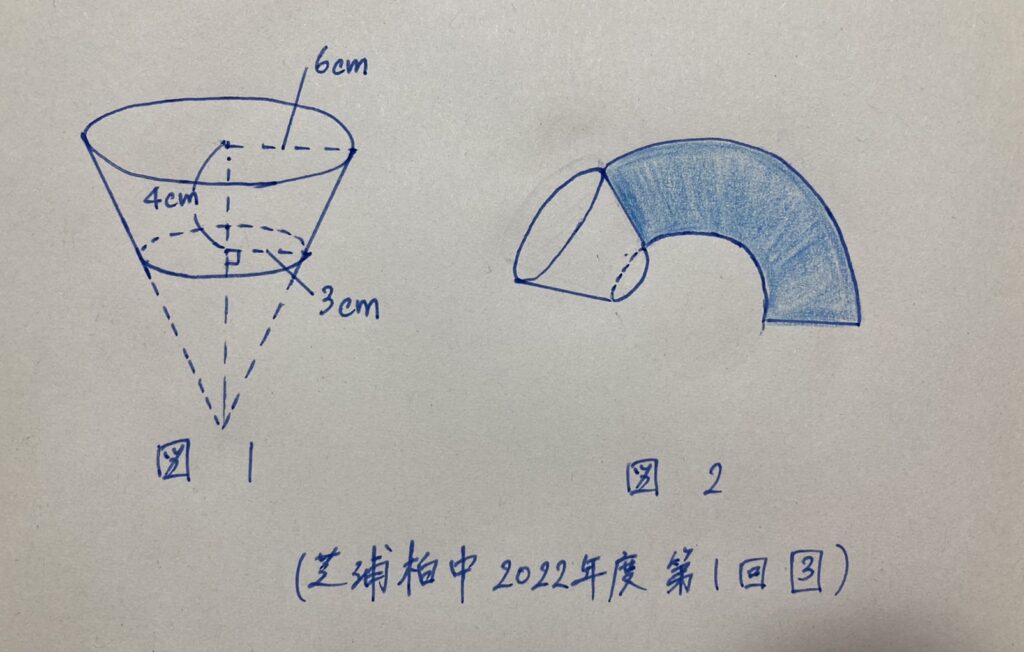
例えば、芝浦柏中の問題で円すい台を転がす問題が大問3に出題されました。
（以下抜粋）
図１のように円すいの1部を切り取った立体があります。この立体の側面にペンキを塗り、立体を図2のように床に転がして色をつけます。ただし、円周率は3.14とします。

(1) 立体がちょうど1周して転がし始めた位置に戻った時、立体は何回転しましたか。
(2) 立体がちょうど1回転した時、床についたペンキの部分の面積は何㎠ですか。

受験者は円すいを回転させる問題は見たことがあるものの、この問題は初めて見るものと仮定します。
受験者の思考は以下の3パターンに分かれると思います。（実際、私の生徒さんの思考もそうでした。）
1. 円すいの一部を切り取って話がややこしくなった。難しそうだから後回しにしよう
2. とりあえず図1の図形の体積を求めてから考えよう
3. 円すいをもとにして考えてみよう

反射的に1と2を選択した方は、相当苦戦すると思います。去年までであれば2の思考で、一旦体積を求めて手がかりを探しに行くと何かしら見つかったのですが、今年は厳しい状態になりました。

3の考え方で、さらに言うと、
立体の回転数→回転といえば1周360度を使うだろう→角度について議論したい→円すいの中心角
と、求めたいものから逆算して必要な情報を集めていく思考法が必要です。

反射的に解く問題ではなく思考を要する問題が、大問３という早い方の問題に出題されたので、全体的に難易度が高くなっていると感じました。

2月に東京受験をされる方は、これからの１週間で応用問題を解いて逆算思考の練習をしていただけたらと思います。