中学受験でよく聞く５年生の壁。学習量、学習内容ともに重くなります。
比と割合が入ってくる２学期以降、理解に時間を要する単元が多いのですが、今回はその前段階のお話です。

先日、Ｓ塾の４年生の方（偏差値５０強）とテキストにある等積変形の問題を解きました。
このような問題です。

三角形ＡＢＣと三角形ＤＥＦは形も大きさも同じ三角形で、点Ｂ，Ｅ，Ｃ，Ｆは一直線上にあります。
長さは図の通りであるとき、ＤＦの長さは何cmですか。

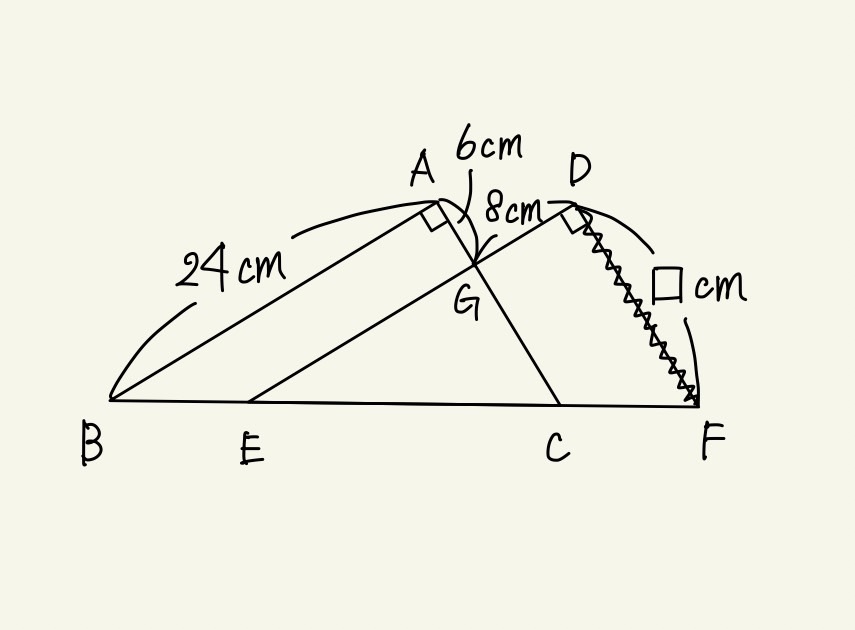
大きさも形も同じ三角形ですから、重複している☆の部分に注目すると、
ア＋☆＝イ＋☆です。つまり、ア＝イの等積変形です。

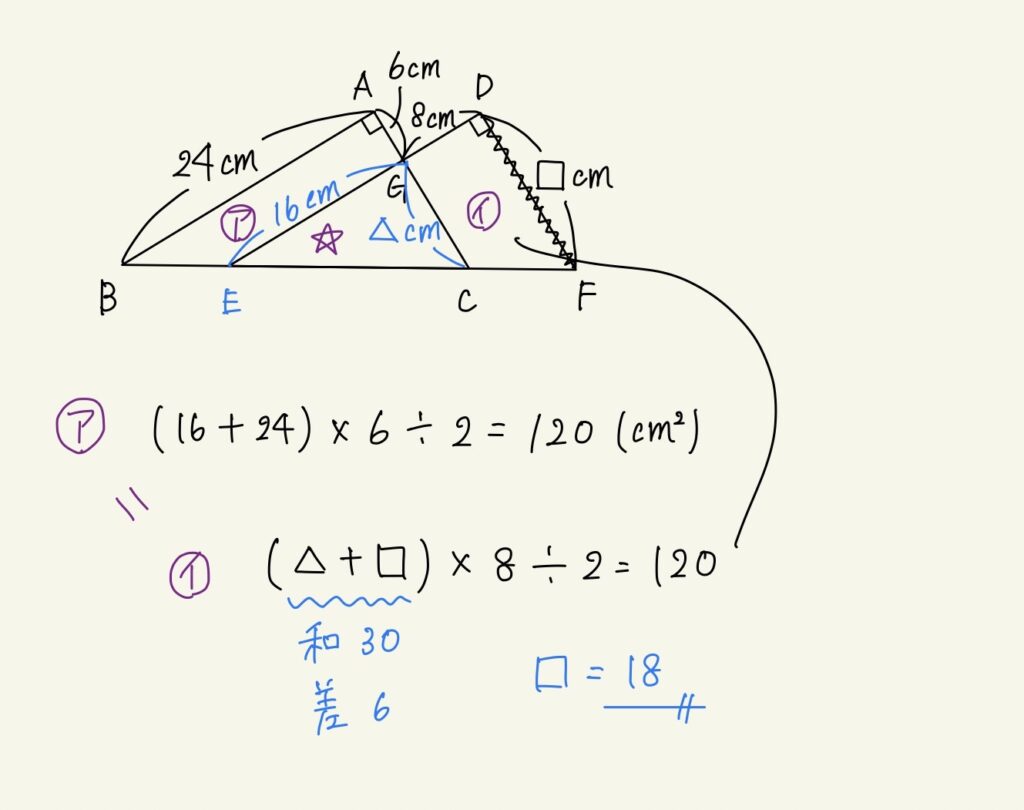
和差算も使う問題で少し難易度は上がるのですが、塾で学習したので生徒さんは正解できました。

１週間後、類題に取り組んでいただきました。

三角形ＡＢＣと三角形ＤＥＦは形も大きさも同じ三角形で、点Ｂ，Ｅ，Ｃ，Ｆは一直線上にあります。
長さと面積は図の通りであるとき、ＢＥの長さは何cmですか。

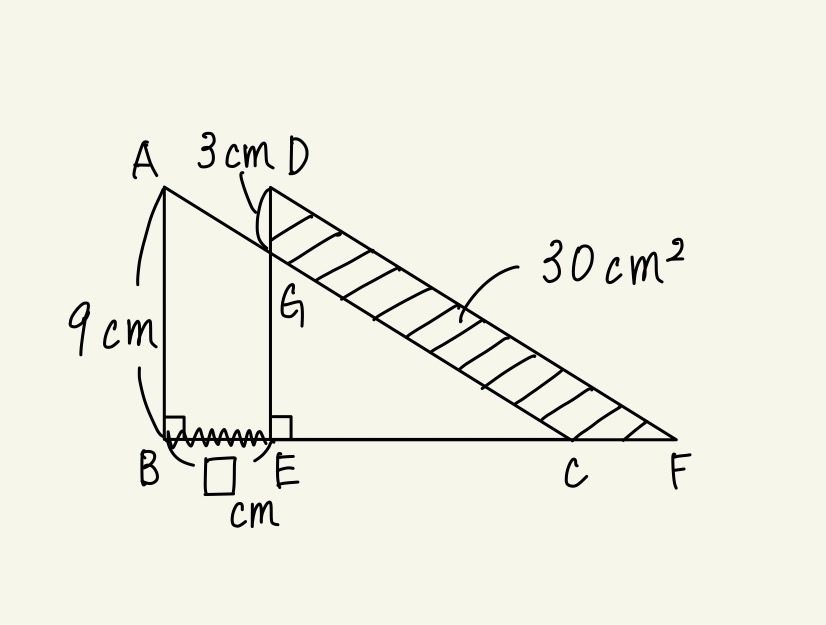
生徒さんの反応は、「見たことあるけど…。面積が突然出てきた、分からない」とのことでした。
違う問題に見えているようです。

そこで、先週学習した問題を見せてどのように解いたかを尋ねました。

生徒「同じとこがかぶってて、アとイが同じ面積だから…」
私　「ストップ。今大事なこと言ったよ。」
生徒「？？」
私　「もう一回言って。」
生徒「同じとこがかぶってて、アとイが同じ面積だから…（２回目）」
私　「今ので解けるよ。図と自分のことばを照らし合わせて考えて」
生徒「あー！同じ面積あった！」

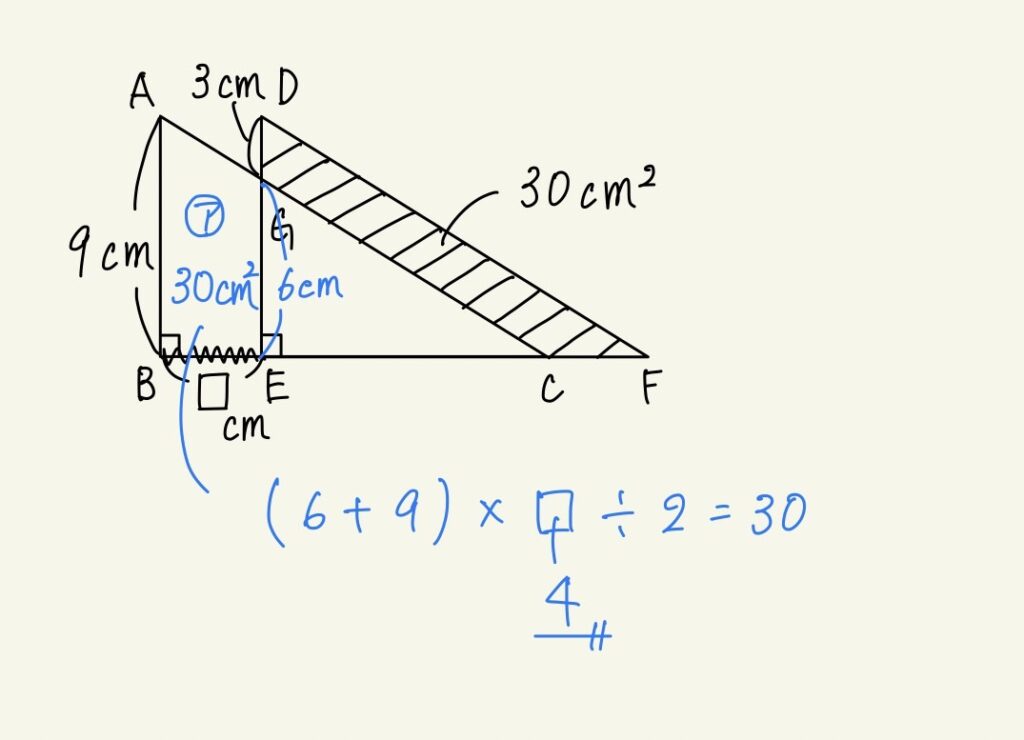
解き方を “一応” 理解しながら解いてはいるものの、単元全体を理解して様々な問題に対応するための「考え方と技術」として身につけていない状態でした。

私のなかで、現在算数の偏差値５０強の生徒さんが、５年生になって徐々に成績を下げていくことが頭をよぎりました。

５年生のテストではテキストと同じ問題がそのまま出題されることがほとんどなくなるので、ポイントとなる考え方を深く理解する必要があります。

学習方法として、問題ごとに「何がポイントか」「どこに注目しなければならないか」を生徒さんに言っていただきます。
しつこいくらい何度も確認することで、上辺だけではない理解に深めていきます。

５年生になって、テキストを３周４周解いても点数に結びつかないケースがありますが、
その場合は学習方法を見直すことで、SAPIX偏差値５０、四谷大塚偏差値５５の壁を超えられると信じています。